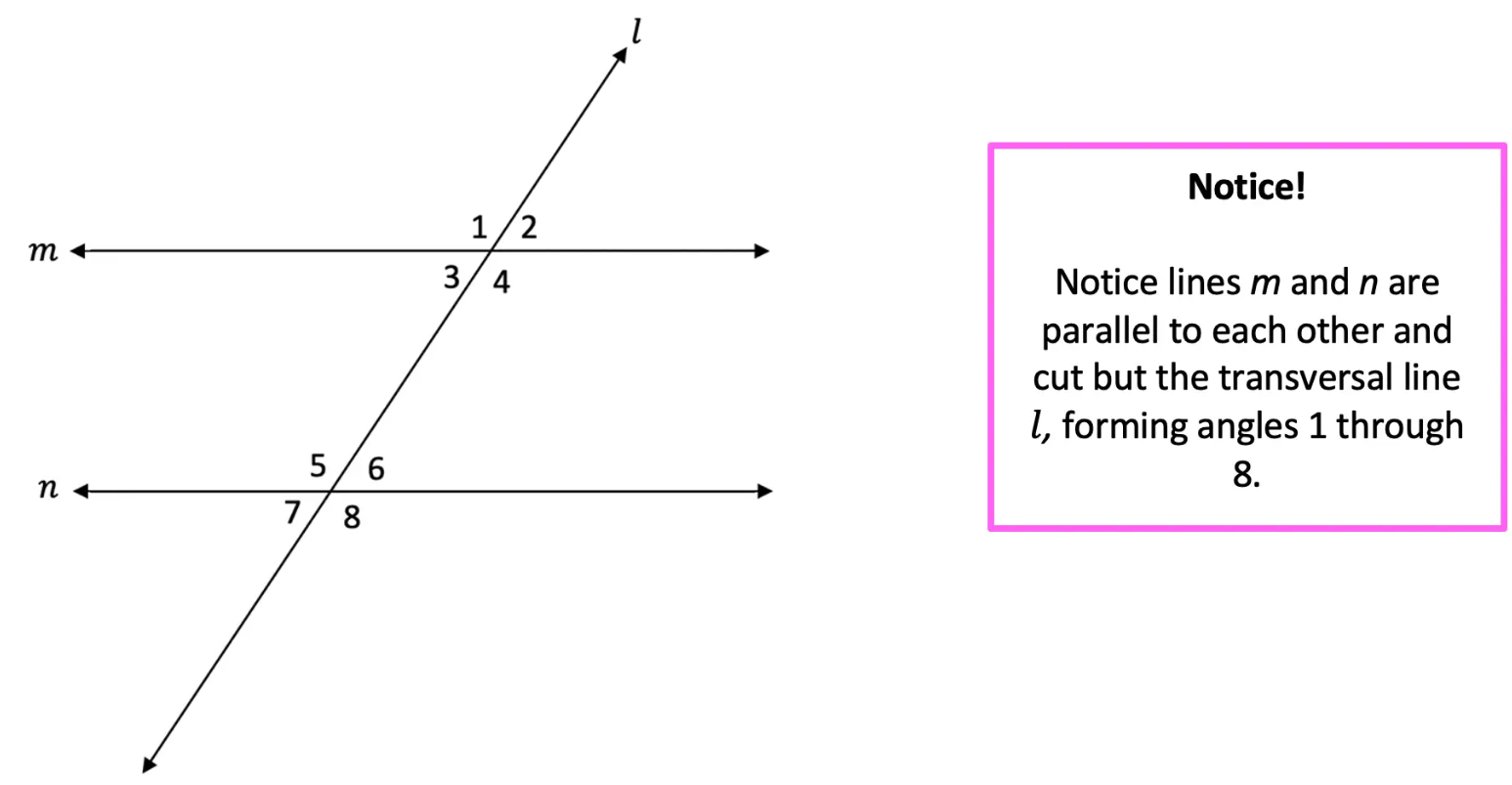
Determining which diagram shows two parallel lines intersected by a transversal is a common geometry question. It tests knowledge of the special angle relationships that result when parallel lines are cut by a transversal. This guide provides a step-by-step method to identify parallel lines cut by a transversal in a diagram using angle theorems and reasoning.
Introduction to Parallel Lines and Transversals
In geometry, parallel lines are two lines in the same plane that never intersect and maintain the same distance between them. A transversal is a third line that intersects two other lines at distinct points.
When a transversal cuts through parallel lines, it forms specific pairs of congruent (equal measure) angles including:
- Corresponding angles – Matching angles on the same side of the transversal and on the same side of the parallel lines.
- Alternate interior angles – The angles between the parallel lines and on opposite sides of the transversal.
- Alternate exterior angles – Outside the parallel lines and on opposite sides of the transversal.
- Same-side interior angles – Inside the parallel lines and on the same side of the transversal. These angles are supplementary (add up to 180°).
Step-by-Step Method to Identify Parallel Lines
When trying to determine which diagram shows parallel lines cut by a transversal, follow these steps:
Step 1) Look for a diagram with two lines crossed by a third line (the transversal).
Step 2) Identify the 8 angles formed by the intersection points. Label each angle if needed.
Step 3) Determine if any angles are already proven congruent based on their angle measure markings.
Step 4) Apply theorems about angles formed by parallel lines cut by a transversal:
- If a pair of corresponding angles are congruent, the lines are parallel.
- If a pair of alternate interior angles are congruent, the lines are parallel.
- If a pair of alternate exterior angles are congruent, the lines are parallel.
- If same-side interior angles are supplementary (add to 180°), the lines are parallel.
Step 5) If one of the above angle conditions is met, conclude the diagram shows parallel lines cut by a transversal.
Examples
Question: Which diagram shows parallel lines cut by a transversal?
Diagram 1:
[Diagram shows two lines intersected by a third line. Angles A and F are marked 115°.]
Diagram 2:
[Diagram shows two lines intersected by a third line. Angles B and E are marked 105°.]
Solution: Diagram 1 shows parallel lines cut by a transversal because the corresponding angles A and F are congruent (both 115°). Since corresponding angles formed by the transversal are congruent, the two crossed lines must be parallel.
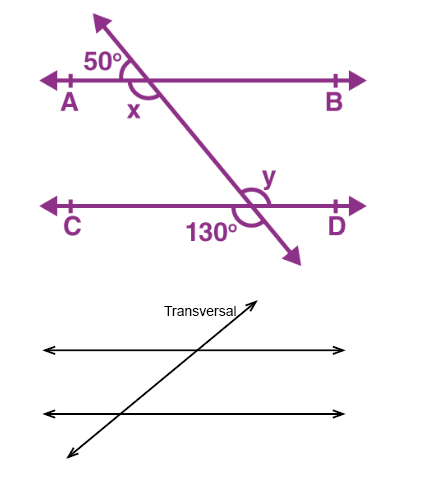
Question: In the diagram below, lines 1 and 2 are cut by transversal t. Does this show parallel lines?
[Diagram shows two lines cut by a transversal. Angles A and D are marked x°. Angle B is marked y°.]
Solution: Yes, this is a diagram of parallel lines cut by a transversal t. Angles A and D are alternate exterior angles and their measures are equal (both x°). The Alternate Exterior Angles Theorem states that if two lines are cut by a transversal and the alternate exterior angles are congruent, then the lines are parallel. Since angles A and D are congruent alternate exterior angles, lines 1 and 2 must be parallel.
Recognizing Non-Parallel Lines Cut by a Transversal
To prove lines are not parallel when cut by a transversal, look for:
- No pairs of congruent corresponding, alternate interior, or alternate exterior angles
- Same-side interior angles that are not supplementary
- Known angle measures that do not obey parallel line angle theorems
- geometric clues like intersecting lines or non-flat angles
If none of the angle conditions indicating parallel lines are met, then the lines cut by the transversal are likely not parallel.
Conclusion
Analyzing angles is the key to determining if a diagram shows two parallel lines intersected by a transversal. Look for congruent corresponding, alternate interior, or alternate exterior angles. Or same-side interior angles that are supplementary. If any of these angle relationships are present, you can conclude the diagram exhibits parallel lines cut by a transversal. Mastering this important geometry skill helps solve many types of parallel line problems.